|
|||||||||||
|
|||||||||||
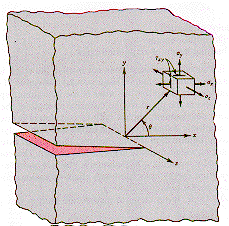
| A
crack tip in a material is the location of a local stress that is larger
than the average stress in the material, a stress concentration. The diagram
shows the stress components acting on an element of material having the
coordinates (r, q)
with respect to a through crack in a sample. The magnitude of these stresses
have the form:
sij = (KI/[2pr]0.5)f(q). KI is known as the stress intensity factor and is defined as KI = Y s (c)0.5, where Y is a geometry dependent constant and c is the crack dimension. Near
the crack tip in the plane of the crack, (r,q)
tend to zero and KI=
(2pr)0.5s,
where
s is the applied tensile
stress. This diverges as r tends to zero. A critical stress intensity factor,
KIc, corresponds to the applied stress reaching the tensile
fracture value, sF.
The relationship between the fracture stress, the crack length, c, and
the fracture toughness, then has the Griffith form:
|
|||||||||||
 |
|||||||||||
| From:
Callister,
"Materials Science and Engineering," Wiley (1994) |
|||||||||||