|
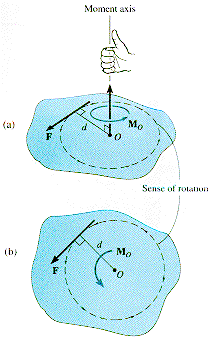
If
a force, F, is at some distance, d, from a point, O, and both are in a
plane (shaded blue in the diagram) then the force is said to have a Moment
of magnitude Mo about the point, where
Mo = Fd.
This moment may be represented by a vector Mo
which is normal to the plane and
directed in the +z direction if the force, F, is in the +x direction of
a Cartesian coordinate system with its origin at O. The distance d is known
as the moment arm of the force and is perpendicular to the direction of
the force.
If
there are several forces in the plane at different distances di from
the point O and with different directions, then the total moment about
O is the sum of the moments due to the individual forces and their moment
arms. If the counter-clockwise direction of the moment is taken to be positive,
moment contributions that are clockwise are taken as negative. MT
= SMo
= (SFidi)
k
, where k
is the unit vector in the +z direction.
Two
parallel but oppositely directed forces of equal magnitude, F, comprise
a "couple." If these forces are a distance, d, apart the moment associated
with the couple is M
= Fd. There is no net force associated with
this moment. |
|
|
|
|
|
|
|
|
|
|
|