| |
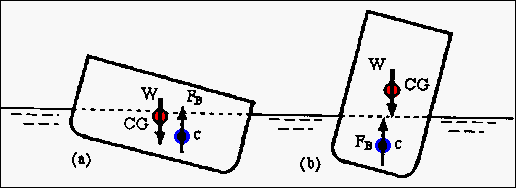
The diagram
below shows the forces acting on the hull of a boat due to the weight
of the hull and the weight of the displaced water. If the boat is floating
at an equilibrium depth in the water, there will be no net force acting on the
hull and the weight, W = mg,
will be equal in magnitude but opposite in direction to the buoyancy
force, FB.
If the hull is floating without any list these two forces will be colinear
and the system will experience no moments due to them.
The
diagram shows two situations that can occurs when the hull is tilted to one side.
In (a) the moment due to the weight and buoyancy acts in a counterclockwise
direction and tends to return the hull to a level position. This hull design
gives a stable ship. In (b) the geometry of the hull causes the center
of buoyancy to move in the other direction as the hull tilts and the moment
due to the weight and buoyancy now acts to increase the tilt of the hull. This
configuration is, therefore, unstable against capsizing.
For a system
in equilibrium there are no net forces and no net moments acting on it. SF = 0, SM = 0 |